FFT

The Fourier transformation is the act of mapping signals from the time domain into the frequency domain. The resulting output is a spectrum showing the frequency content of the original signal.

The formula for a discrete Fourier transform (DFT) is as follows:

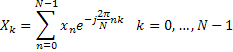
The DFT is very computational intensive. Each frequency component X(k) requires N complex multiplications and N complex additions. If there are N frequency components, an N-point DFT has a computational complexity of 2N^2.  However a fast Fourier transform uses several different optimizations, like the butterfly method shown below, to reduce the total number of operations to N logN.

This was my original attempt at designing my own 32-point FFT module.

The address generation unit (AGU) would control the memory content sent to and from the butterfly processor. Since the FPGA RAM function only has two two read and write ports, this design uses two separate RAM blocks. The general idea is that the system reads from one RAM block, processes through the butterfly unit and writes to the other RAM block. Here the high level box diagram of the dual port RAMs used in my design:

The FFT core from altera contains nearly 140 different files, you can check it out on me github repository here here